A control system is a group of equipment that manages, orders, guides, or controls the actions of other devices in order to produce a specific outcome. To put it another way, a control system can be defined as a system that directs other systems to reach a specific state. There are many different kinds of control systems, and they can be broadly divided into
- Linear control systems and
- Non-linear control systems.
Below, several different control systems are covered in more detail.
Linear Control System:
Voltage and current characteristics are linear in a linear control system. This assumes that each network piece will behave in a perfect manner and ignores all undesirable effects (which is only conceivable in theories). The principles of homogeneity and additivity are followed by the linear control system. The output in this case equals the input.If a system adheres to the superposition and homogeneity principles, it is considered to be linear.
The Homogeneity Principle:
According to the concept of homogeneity, a system that creates an output for an input x(t) must also generate an output for an input ax(t) (t).
Superposition Theory:
The concept of superposition states that a system must create an output [y1(t) + y2(t)] for an input [x1(t) + x2(t)] if it produces an output y1(t) for an input x1(t) and an output y2(t) for an input x2(t).
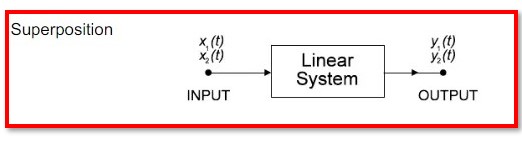
Consequently, given a linear system with continuous time and a linear discrete-time system.
Therefore, a system is said to be linear if the output it produces as a result of the weighted sum of its inputs equals the weighted sum of its outputs.
Additivity:
Assume that have a system S, first provide it with input as a1, and receive the output as b1, which corresponds to input a1. Giving input a2 a second time results in output b2 in accordance with this.
Examples of Linear System:
- Communication channels,
- A network that is solely resistive and has a steady DC source
- Filter circuits, and others.
These circuits adhere to the additivity, superposition theory, and homogeneity principles. All undesirable effects are disregarded, and by assuming that every network component will behave perfectly, claims that it will obtain linear voltage and current characteristics. This serves as an illustration of a linear control system.
Non-Linear Control System:
If a system violates the homogeneity and superposition principles, it is said to as a nonlinear system.The system will typically be a non-linear system if the equation defining it comprises square or higher order terms of input/output, product of input/output and its derivatives, or a constant.
Examples of Non-Linear System:
- An example of a non-linear system is the triangulation of GPS signals.
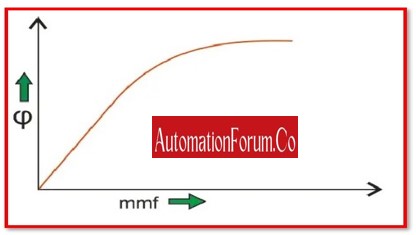
- A magnetization curve or the no load curve of a DC machine are well-known examples of non-linear systems. Here, we shall quickly explain the no-load curve of DC devices. The link between the air gap flux and the field winding mmf is not provided by a load curve. The curve shown below makes it abundantly evident that there is initially a linear relationship between the winding mmf and the air gap flux, but that this relationship changes when saturation occurs, revealing the nonlinear behaviour of the curve or features of the nonlinear control system.
Analog / Continuous System:
We use a continuous signal as the system input in these kinds of control systems. These signals represent a continuous time function. We may have a variety of sources for continuous input signals, including sources for square and sinusoidal signals, sources for continuous triangle signals, and more.
Discrete / Digital System:
A discrete signal (or a signal that may take the shape of a pulse) serves as the system input in these kinds of control systems.There is a defined time period for these signals. Using the switch, we may transform a variety of continuous input signal sources—such as sinusoidal and square signal input sources, among others—into a discrete form.
Discrete or digital systems currently have a number of advantages over analogue systems, some of which are listed below:
Comparatively to analogue systems, digital systems are better able to handle nonlinear control systems.When opposed to analogue systems, discrete or digital systems consume less power.
In comparison to analogue systems, digital systems are more accurate and can carry out a variety of sophisticated computations with ease.When compared to an analogue system, the digital system is more reliable. Additionally, they are compact and modest in size.
Digital systems operate logically, which greatly improves their correctness. Losses in discrete systems are generally lower than those in analogue systems.
Systems with a Single Input and Output:
These are also referred to as SISO systems. This system just has one input and one output. Temperature control, position control systems, and more examples of this kind of system are possible.
Systems with a Multiple Input and Output:
These are also referred to as MIMO systems. This system has numerous outputs for numerous inputs. Examples of this type of system include PLC-type systems and others.
Lumped Parameter System:
These sorts of control systems are known as lumped parameter systems because it is thought that all of the active and passive components are concentrated at a single location in these systems. Such systems are fairly simple to analyse using differential equations.
Distributed Parameter System:
The term “distributed parameter type of system” refers to the assumption that the various active (such as inductors and capacitors) and passive (such as resistor) parameters are spread uniformly along the length in these sorts of control systems. It is a little challenging to analyse this kind of system using partial differential equations.





