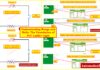
The phrase “wet leg” refers to a system where the transmitter low pressure side impulse line is completely filled with liquid (typically the same liquid as the process).

A tiny catch tank is located at the head of the low pressure impulse line. The petrol phase or vapors will condense in the catch tank and wet leg. On the low pressure side of the level transmitter, the catch tank and the incline connecting line provide a constant hydrostatic pressure. As this pressure is consistent, calibration makes it simple to account for it.
h = Process Level range need to be measured
x = Height of the wet leg
S.G1 = Specific gravity of the process liquid
S.G2 = Specific gravity of the filled liquid in wet leg
Pressure on H.P. side of transmitter P.HP = Pgas + (SG1*h)
Pressure on LP side of the transmitter P.LP= Pgas + (SG2*x)
The transmitter’s differential pressure is calculated as follows:
DP = P.HP – P.LP
DP = {Pgas + (SG1*h)} – {Pgas + (SG2*x)}
DP = (SG1*h) – (SG2*x)
LRV Calculation
Calculate the Differential pressure (DP) when the tank is empty (h=0).
PH.P = Pgas + (SG1*h)
PL.P = Pgas + (SG2*x)
LRV = PH.P. – PL.P
LRV = {Pgas + (SG1*h)} – {Pgas + (SG2*x)}
LRV = {Pgas + (SG1*0)} – {Pgas + (SG2*x)}
LRV = – (SG2*x)
Estimating the URV
Determine the Differential pressure (DP) of the transmitter when the tank level is reached to the maximum range with process liquid (h) .
PH.P = Pgas + (SG1*h)
PL.P = Pgas + (SG2*x)
URV = PH.P. – PL.P
URV = {Pgas + (SG1*h)} – {Pgas + (SG2*x)}
URV = {(SG1*h) – (SG2*x)}
Range of the transmitter = – (SG2*x) to {(SG1*h) – (SG2*x)}
DP calculator for Wet leg Level measurement – Transmitter installed in zero based direct mount application
Click here for more Instrumentation Calculators